Longest Sub{string,array}

Prospect:

https://leetcode.com/problems/length-of-the-longest-alphabetical-continuous-substring/description/

Longest Consecutive x with k impurities (1-pass)

while shrink

Generic Solution: Longest Consecutive x with k Impurities (1-pass)

Solution

The goal is to identify the longest subarray within nums where the allowed value allowed appears consecutively, with up to k impurities (elements other than allowed). An impurity refers to any element in the array that differs from the specified allowed value. This is addressed using a variable-size sliding window technique that dynamically adjusts to maintain a valid subarray according to the problem’s constraints.

Expansion:

• The window expands by incrementing the right pointer. If the current element (nums[right]) is not allowed, increment the impurity count (count).

• This stage progressively includes more elements into consideration for forming the longest valid subarray.

Shrinking:

• The window shrinks from the left by incrementing the left pointer, reducing the impurity count as necessary to ensure the subarray remains valid (i.e., count does not exceed k).

• The shrink process continues until the subarray meets the constraint of having at most k impurities, making it valid for evaluation.

Logic:

• After ensuring the current subarray is valid, update maxi to capture the length of the longest subarray found that satisfies the given conditions.

The solution iteratively adjusts the window size to explore all possible valid subarrays, ultimately returning the length of the longest one found.

Implementation Notes

• Impurities are defined as elements within the subarray that differ from the allowed value. The presence of more than k impurities invalidates the current subarray.

• The expansion phase is handled incrementally with each iteration of the while right < n loop, ensuring a gradual exploration of the array.

• The shrinking phase is crucial for maintaining the validity of the subarray, using a while loop to adjust the window size until the impurity constraint is satisfied.

• The approach emphasizes ensuring the subarray is valid before applying the problem-specific logic, a common intuition behind many sliding window problems.

Analysis

Time Complexity: O(N)

• The algorithm iterates through each element of nums once, making adjustments to the sliding window as needed, leading to linear time complexity.

Space Complexity: O(1)

• Constant extra space is utilized, with a few variables to track the window boundaries, impurity count, and maximum length found.

Python

def longestAllowed(self, nums: List[Any], allowed: Any, k: int) -> int:
    n = len(nums)
    left = right = 0
    count = maxi = 0
    while right < n:
        # Expansion
        if nums[right] != allowed:
            count += 1
        right += 1
        # Shrinking
        while left < right and count > k:
            if nums[left] != allowed:
                count -= 1
            left += 1
        # Make sure the subarray is valid which abides all constraints of the problem statement
        # That is, subarray should have at most 'k' impurities (other than allowed 'x')
        maxi = max(maxi, right - left)
    return maxi

1004. Max Consecutive Ones III (Medium)

Solution

The challenge is to find the maximum number of consecutive 1’s in the array nums after flipping at most k zeros to 1’s. This problem is effectively solved using a variable-size sliding window approach that dynamically adjusts to include as many 1’s as possible while allowing up to k zeros within the window.

The solution iterates through nums, expanding the window to include consecutive elements and using a counter (zeros) to track the number of zeros within the current window. The window shrinks as necessary to ensure that the count of zeros does not exceed k, thereby maintaining the validity of the window according to the problem’s constraints.

Expansion:

• Increment the right pointer to expand the window, increasing the zeros counter if the current element is a zero.

Shrinking:

• If the zeros count exceeds k, increment the left pointer to shrink the window from the left, decrementing the zeros counter if a zero leaves the window. This step ensures the window remains valid under the given constraint.

Logic:

• After each adjustment, calculate the current window’s length (right - left) if it is valid (i.e., contains at most k zeros). Update maxi to keep track of the maximum length found.

The function returns maxi, representing the length of the longest valid subarray found that satisfies the condition of having at most k zeros, effectively maximizing the number of consecutive 1’s.

Analysis

Time Complexity: O(N)

• The algorithm iterates through the array nums once, with each element being considered for inclusion in the window exactly once. The linear scan, combined with efficient window adjustments, results in linear time complexity.

Space Complexity: O(1)

• Constant extra space is utilized, with variables to track the window boundaries (left and right), the count of zeros within the window (zeros), and the maximum window length found (maxi).

Python

def longestOnes(self, nums: List[int], k: int) -> int:
    n = len(nums)
    left = right = 0
    zeros = maxi = 0
    while right < n:
        # Expansion
        zeros += nums[right] == 0
        right += 1
        # Shrinking: until zeros<=k
        while left < right and zeros > k:
            zeros -= nums[left] == 0
            left += 1
        # Logic
        # Make sure the subarray is valid which abides all constraints of the problem statement
        # That is, subarray should have at most 'k' zeros
        maxi = max(maxi, right - left)
    return maxi

Using Generalized Approach:

Python

def longestOnes(self, nums: List[int], k: int) -> int:
    return self.longestAllowed(nums, allowed=1, k=k)

487. Max Consecutive Ones II (Medium)

Solution

This problem extends “Max Consecutive Ones” by allowing for at most one zero to be flipped to one, thereby increasing the length of a consecutive ones sequence. It can be directly solved by applying the generic solution longestAllowed, designed to find the longest sequence of a specified value (allowed = 1) with a tolerance for a limited number of impurities (k = 1).

The longestAllowed function, previously detailed, is adept at identifying the longest subarray meeting specific criteria—here, the maximum number of consecutive 1’s with up to one 0 allowed. By setting allowed to 1 and k to 1, the generic solution becomes tailored to this problem’s requirements.

Implementation:

• The solution is a straightforward application of the longestAllowed function, passing nums as the input array, allowed as 1 (target value), and k as 1 (allowing for one impurity, i.e., one zero to be flipped).

The function call self.longestAllowed(nums, allowed=1, k=1) returns the maximum length of a subarray in nums that consists of consecutive 1’s, considering that at most one 0 can be flipped to 1, directly addressing the “Max Consecutive Ones II” challenge.

Analysis

Time Complexity: O(N)

• Leveraging the longestAllowed function involves a single pass through the array nums, adjusting the sliding window as necessary to find the longest valid subarray, thus ensuring linear time complexity.

Space Complexity: O(1)

• The space complexity is constant, as the generic solution utilizes a fixed number of variables for its operation, independent of the input size.

Python

def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
    return self.longestAllowed(nums, allowed=1, k=1)

485. Max Consecutive Ones (Easy)

Solution

The problem seeks to identify the longest sequence of consecutive 1’s in the given binary array nums. This can be seamlessly addressed by the longestAllowed function, which is adept at locating the longest sequence of a specified value with a tolerance for a given number of impurities. For this problem, the allowed value is 1, and since no impurities (0’s) are permitted in the sequence, k is set to 0.

Implementation:

• Invoke the longestAllowed function with nums as the array to search, allowed as 1 to specify the target value, and k as 0 to indicate that no deviations from the target value are allowed. This effectively tailors the generic solution to find the longest sequence of consecutive 1’s without any interruptions by 0’s.

The function call self.longestAllowed(nums, allowed=1, k=0) directly computes the maximum length of a subarray in nums comprising consecutive 1’s, fitting the problem’s criteria perfectly.

Analysis

Time Complexity: O(N)

• Utilizing the longestAllowed function involves a single traversal through the array nums, with the sliding window adjusting as needed to identify the longest valid subarray. This approach guarantees linear time complexity.

Space Complexity: O(1)

• Constant space is utilized by the solution, as the generic method employs a fixed number of variables to conduct its operation, irrespective of the input array’s size.

Python

def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
    return self.longestAllowed(nums, allowed=1, k=0)

1493. Longest Subarray of 1’s After Deleting One Element (Medium)

Solution

This problem seeks the longest subarray of 1’s achievable by removing exactly one element from a binary array nums. The solution employs the longestAllowed function, apt for finding the longest sequence of a specified value with a limited number of impurities, here tailored to allow for one “impurity” (k = 1). An “impurity” in this context refers to a zero that can be “removed” or flipped to maintain a continuous sequence of ones.

However, the problem includes specific conditions that necessitate slight adjustments:

• If nums consists entirely of 1’s, removing one element (a 1) results in a subarray one element shorter than the original array (n - 1).

• In other cases, the longest sequence of 1’s with at most one 0 is found using longestAllowed. The length of the subarray after deletion equates to right - left - 1, accounting for the removal of one 0.

The element to be deleted can either be a 1 or a 0, affecting the calculation of the longest valid subarray.

Implementation:

• Apply longestAllowed with nums as the array, allowed = 1 for targeting sequences of 1’s, and k = 1 for permitting one zero. The final result adjusts for the removal of one element by subtracting 1 from the computed length.

The function call self.longestAllowed(nums, allowed=1, k=1) - 1 computes the length of the longest subarray of 1’s possible after one deletion, conforming to the problem’s specifications.

Analysis

Time Complexity: O(N)

• A single traversal through nums is conducted by the longestAllowed function, with linear time complexity ensured.

Space Complexity: O(1)

• Constant space is utilized for the operation, as the solution employs a minimal number of variables, regardless of the input array’s size.

Python

def longestSubarray(self, nums: List[int]) -> int:
    return self.longestAllowed(nums, allowed=1, k=1) - 1

---

Longest Consecutive x with k impurities (>1-pass)

while shrink

1869. Longer Contiguous Segments of Ones than Zeros (Easy)

Solution

The goal is to determine if the longest contiguous segment of 1’s in the binary string s is longer than the longest contiguous segment of 0’s. This involves addressing two subproblems:

• Finding the longest consecutive sequence of "1"’s.

• Finding the longest consecutive sequence of "0"’s.

Each subproblem can be solved by applying the longestAllowed function, originally designed to find the longest sequence of a specified value in an array, here adapted to work with binary strings. For this problem, the function is invoked twice, once for "1"’s and once for "0"’s, each time with k = 0 to ensure only contiguous segments are considered.

Implementation:

• Calculate the length of the longest consecutive "1"’s using longestAllowed(s, allowed="1", k=0).

• Similarly, calculate the length of the longest consecutive "0"’s using longestAllowed(s, allowed="0", k=0).

• Compare the lengths of these segments to determine if the segment of "1"’s is longer than that of "0"’s.

The function checkZeroOnes returns True if the longest contiguous segment of "1"’s is greater than that of "0"’s, indicating the binary string s contains longer segments of 1’s than 0’s, as per the problem’s requirements.

Analysis

Time Complexity: O(N)

• The longestAllowed function is called twice, each time requiring a pass through the string s. Despite the two passes, the overall complexity remains linear in the length of s.

Space Complexity: O(1)

• The space used is constant, as the solution requires only variables to track the lengths of the longest segments and does not depend on the size of the input string.

Python

def checkZeroOnes(self, s: str) -> bool:
    ones = self.longestAllowed(s, allowed="1", k=0)
    zeros = self.longestAllowed(s, allowed="0", k=0)
    return ones > zeros

2024. Maximize the Confusion of an Exam (Medium)

Generic Approach1 Pass

Solution

The objective is to find the maximum number of consecutive correct answers (‘T’s) that can be achieved on an exam by flipping at most k incorrect answers (‘F’s) to correct (‘T’s), or vice versa. This entails addressing two subproblems:

• Finding the longest sequence of consecutive "T"’s with at most k "F"’s replaced.

• Finding the longest sequence of consecutive "F"’s with at most k "T"’s replaced.

Each subproblem can be efficiently solved by applying the longestAllowed function, which is designed to find the longest sequence of a specified value with a tolerance for a limited number of impurities, here adapted for binary strings. For this problem, k impurities (either ‘T’ or ‘F’) are allowed to be replaced to maximize the sequence length.

Implementation:

• Calculate the longest sequence of "T"’s by treating "F"’s as impurities and allowing up to k of them to be replaced, using longestAllowed(answerKey, allowed="T", k=k).

• Similarly, calculate the longest sequence of "F"’s by treating "T"’s as impurities and allowing up to k replacements, using longestAllowed(answerKey, allowed="F", k=k).

• Return the maximum of these two lengths to determine the maximum confusion (i.e., the maximum number of consecutive correct answers achievable through replacements).

The function maxConsecutiveAnswers returns the maximum achievable length of consecutive correct answers by optimally using replacements, as per the problem’s requirements.

Analysis

Time Complexity: O(N)

• The longestAllowed function is invoked twice—once for each possible value (‘T’ and ‘F’)—each requiring a single pass through the answerKey string. Despite the dual invocations, the overall time complexity remains linear in the length of answerKey.

Space Complexity: O(1)

• Constant space is utilized, as the solution leverages a fixed number of variables to track the lengths of the longest segments and does not depend on the size of the input string.

Python

def maxConsecutiveAnswers(self, answerKey: str, k: int) -> int:
    max_con_T = self.longestAllowed(answerKey, allowed="T", k=k)
    max_con_F = self.longestAllowed(answerKey, allowed="F", k=k)
    return max(max_con_T, max_con_F)

424. Longest Repeating Character Replacement (Medium)

Generic Approach1 Pass

Solution

To maximize the length of a subarray where after replacing at most k characters, all characters in the subarray are the same, we iteratively apply the longestAllowed function across all unique characters in the string s. This accounts for two subproblems:

• Finding the longest consecutive sequence of each character when at most k different characters are replaced.

• Comparing these lengths to determine the maximum achievable sequence length.

Implementation:

• For each unique character in s, calculate the longest sequence achievable by allowing up to k replacements of other characters, using longestAllowed.

• Determine the maximum length from these calculations to find the overall longest sequence after replacements.

The function characterReplacement returns the length of the longest subarray after replacements, optimized across all unique characters in s.

Analysis

Time Complexity: O(N * M)

• N is the length of string s, and M is the number of unique characters. The longestAllowed function is invoked once per unique character, each time requiring a pass through s.

Space Complexity: O(M)

• The space complexity depends on the storage required for tracking the longest sequences for each character, which is proportional to the number of unique characters.

Python

def characterReplacement(self, s: str, k: int) -> int:
    maxi = 0
    for char in set(s):
        maxi = max(maxi, self.longestAllowed(s, allowed=char, k=k))
    return maxi

---

Hashmap - Unique Elements

while shrink

3. Longest Substring Without Repeating Characters (Medium)

Solution

The task is to find the length of the longest substring of a given string s that does not contain any repeating characters. This challenge is efficiently addressed using a sliding window approach coupled with a counter to track the frequency of characters within the current window.

The solution iterates through s, dynamically adjusting the window to always encompass a substring without repeating characters. The counter ensures that each character’s occurrence is monitored, facilitating the identification of unique substrings.

Expansion:

• The window expands by including the current character and updating its frequency in the counter as the right pointer advances.

Shrinking:

• If a character repetition is detected (not is_unique()), the window shrinks from the left by decrementing the left pointer and adjusting the counter accordingly. This process continues until the substring within the window is unique again.

Logic:

• After each expansion (or necessary shrinking), the length of the current valid (unique) window (right - left) is compared against maxi, the maximum length encountered so far, and maxi is updated if a longer unique substring is found.

The function lengthOfLongestSubstring returns maxi, representing the length of the longest substring without repeating characters found within s.

Analysis

Time Complexity: O(N)

• The algorithm performs a single pass through the string s, with each character being considered exactly once for inclusion in the window. Adjustments to the window size and the counter are done in constant time, ensuring linear time complexity.

Space Complexity: O(26)

• The space complexity is determined by the size of the counter, which tracks the frequency of characters within the window. At worst case, s can contain all lower case alphabets.

Python

def lengthOfLongestSubstring(self, s: str) -> int:
    n = len(s)
    left = right = 0
    counter = collections.Counter()
    maxi = 0

    is_unique = lambda: len(counter) == right - left

    while right < n:
        # Expansion
        counter[s[right]] += 1
        right += 1
        # Shrinking
        while left < right and not is_unique():
            counter[s[left]] -= 1
            if counter[s[left]] == 0:
                counter.pop(s[left])
            left += 1
        # Logic
        maxi = max(maxi, right - left)
    return maxi

1695. Maximum Erasure Value (Medium)

Solution

Can be restated as “Find the maximum sum of subarray with unique elements”.

The goal is to find the maximum score you can obtain by erasing a subarray from a given array nums. The score of a subarray is the sum of its elements, and the subarray to be erased must contain unique elements. This problem can be effectively solved using a sliding window approach, complemented by a counter to track the elements within the current window and ensure their uniqueness.

The solution iterates through nums, dynamically adjusting the window to always encompass a subarray with unique elements. The counter aids in monitoring each element’s presence within the window, while total keeps track of the current window’s score.

Expansion:

• The window expands by incorporating the current element into total and updating its frequency in the counter as the right pointer moves forward.

Shrinking:

• If a repetition is detected (not is_unique()), the window shrinks from the left by decrementing the left pointer, adjusting the counter, and subtracting the element’s value from total. This continues until the window regains uniqueness.

Logic:

• After each adjustment, compare the current total against maxi, updating maxi if a higher score is found. This ensures the maximum erasure value is recorded.

The function maximumUniqueSubarray returns maxi, the highest score obtainable by erasing a unique subarray from nums.

Analysis

Time Complexity: O(N)

• A single pass through nums is conducted, with each element being considered for inclusion in the window exactly once. The linear scan, combined with constant-time operations for each element (expansion, shrinking, and updating total and maxi), results in linear time complexity.

Space Complexity: O(26)

• The space complexity is determined by the size of the counter, which tracks the frequency of characters within the window. At worst case, s can contain all lower case alphabets.

Python

def maximumUniqueSubarray(self, nums: List[int]) -> int:
    n = len(nums)
    left = right = 0
    counter = collections.Counter()
    maxi = total = 0

    is_unique = lambda: right - left == len(counter)

    while right < n:
        # Expansion
        counter[nums[right]] += 1
        total += nums[right]
        right += 1
        # Shrinking
        while left < right and not is_unique():
            counter[nums[left]] -= 1
            total -= nums[left]
            if counter[nums[left]] == 0:
                counter.pop(nums[left])
            left += 1
        # Logic
        maxi = max(maxi, total)
    return maxi

---

Hashmap - K Distinct Elements

while shrink

340. Longest Substring with At Most K Distinct Characters (Medium)

Solution

This problem aims to find the length of the longest substring that contains at most k distinct characters from a given string s. The challenge is efficiently addressed using a sliding window technique, complemented by a counter to track the frequency of each character within the current window.

The solution iterates through s, expanding the window to include more characters and using the counter to ensure the distinct character count within the window does not exceed k.

Expansion:

• The window expands by including the current character in the counter as the right pointer advances, incrementing the character’s count.

Shrinking:

• If the distinct character count within the window exceeds k, the window shrinks from the left by decrementing the left pointer and adjusting the counter accordingly. This process continues until the window again contains at most k distinct characters.

Logic:

• After each expansion (or necessary shrinking), the length of the current valid window (right - left) is compared against maxi, the maximum length encountered so far, and maxi is updated if a longer substring is found.

The function lengthOfLongestSubstringKDistinct returns maxi, representing the length of the longest substring within s that contains at most k distinct characters.

Analysis

Time Complexity: O(N)

• The algorithm performs a single pass through the string s, with each character being considered exactly once for inclusion in the window. Adjustments to the window size and the counter are done in constant time, ensuring linear time complexity.

Space Complexity: O(k)

• The space complexity is influenced by the counter, which tracks the frequency of characters within the window. In the worst case, the counter could contain up to k distinct characters, indicating the space requirement is proportional to k.

Python

def lengthOfLongestSubstringKDistinct(self, s: str, k: int) -> int:
    n = len(s)
    left = right = 0
    counter = collections.Counter()
    maxi = 0

    # Function to check if the window contains at most k distinct characters
    k_distinct = lambda: len(counter) <= k

    while right < n:
        # Expansion: Include the current character and update its count
        counter[s[right]] += 1
        right += 1
        # Shrinking: Ensure the window does not exceed k distinct characters
        while left < right and not k_distinct():
            counter[s[left]] -= 1
            if counter[s[left]] == 0:
                counter.pop(s[left])
            left += 1
        # Update the maximum length found so far
        maxi = max(maxi, right - left)
    return maxi

159. Longest Substring with At Most Two Distinct Characters (Medium)

Solution

This problem is a specific instance of the broader challenge tackled in 340. Longest Substring with At Most K Distinct Characters (Medium) where k is set to 2. The task is to identify the length of the longest substring in a given string s that contains at most two distinct characters. By setting k = 2, we apply the previously outlined sliding window and counter strategy to solve this specialized version efficiently.

The solution directly utilizes the lengthOfLongestSubstringKDistinct function, previously described, by passing k = 2 as an argument. This adaptation allows for the same dynamic window adjustment and character tracking methodology to be employed, focusing on ensuring that no more than two distinct characters are present in any considered substring.

Implementation:

• The lengthOfLongestSubstringKDistinct function is invoked with s as the input string and k set to 2. This approach seamlessly tailors the generic solution to meet the specific requirements of this problem, leveraging the logic developed for handling up to k distinct characters in a substring.

The function lengthOfLongestSubstringTwoDistinct returns the maximum length of a substring in s that complies with the constraint of containing at most two distinct characters.

Analysis

Time Complexity: O(N)

• Invoking lengthOfLongestSubstringKDistinct with k = 2 entails a single pass through the string s, with linear time complexity ensured by the efficient sliding window and counter adjustments.

Space Complexity: O(k) = O(2) = O(1)

• The space complexity is effectively constant, as the number of distinct characters tracked by the counter is limited to at most two in this specific scenario. This constraint bounds the additional space required, irrespective of the length of s.

Python

def lengthOfLongestSubstringTwoDistinct(self, s: str) -> int:
    return self.lengthOfLongestSubstringKDistinct(s, k=2)

904. Fruit Into Baskets (Medium)

Solution

A special case of 340. Longest Substring with At Most K Distinct Characters (Medium), where k = 2.

Also, literally similar to 159. Longest Substring with At Most Two Distinct Characters (Medium), but in different words.

Analysis

Time Complexity: O(N)

Space Complexity: O(k) = O(2) = O(1)

Python

def totalFruit(self, fruits: List[int]) -> int:
    return self.lengthOfLongestSubstringKDistinct(fruits, k=2)

1446. Consecutive Characters (Easy)

Solution

This problem asks for the maximum power of a string s, defined as the maximum length of a non-empty substring that contains only one unique character. This problem is a specific instance of finding the longest substring with at most k distinct characters, where k = 1.

By utilizing the lengthOfLongestSubstringKDistinct function, which was designed to find the longest substring with up to k distinct characters, we can directly apply it to solve this problem. Setting k = 1 allows for the identification of the longest sequence of consecutive identical characters, aligning perfectly with the problem’s requirements.

Implementation:

• Invoke lengthOfLongestSubstringKDistinct with s as the input string and k = 1 to specifically target sequences of consecutive identical characters.

• This method dynamically adjusts a sliding window to encompass the longest substring that satisfies the condition of having at most one distinct character.

The function maxPower leverages this approach to calculate the maximum power of s, effectively determining the length of the longest substring composed of consecutive identical characters.

Analysis

Time Complexity: O(N)

• Employing lengthOfLongestSubstringKDistinct with k = 1 entails a single traversal through the string s, maintaining linear time complexity due to the efficient sliding window mechanism.

Space Complexity: O(1)

• The space complexity is constant, as the solution uses only a few variables for tracking the window’s boundaries and the maximum substring length, independent of the input string’s size.

Python

def maxPower(self, s: str) -> int:
    return self.lengthOfLongestSubstringKDistinct(s, k=1)

---

Depends on prev

while expand

674. Longest Continuous Increasing Subsequence (Easy)

Solution

The aim is to identify the length of the longest continuous increasing subsequence (LCIS) within an array nums. This challenge is effectively approached using a sliding window technique, tracking the current subsequence’s start and end points while monitoring for any breaks in the increasing sequence.

The solution iterates through nums, expanding the window to encompass consecutive elements that form an increasing sequence. The prev variable is used to compare the current element against the last, ensuring continuity in the increasing order.

Expansion:

• The window expands by moving the right pointer forward, as long as the current element is greater than the previous one (prev, essentially nums[right - 1]). The prev variable is updated to reflect the most recent element in the sequence.

Logic:

• After each expansion or when an increasing sequence is interrupted, calculate the current window’s length (right - left) and compare it against maxi, updating maxi if a longer subsequence is found.

Shrinking:

• Upon encountering an element that does not continue the increasing sequence, set prev to the current element (or None if at the end of the array)

• Shrinking is done rapidly but without while loop. For the next expansion, left starts from the current right. To avoid infinite outer while loop when right is never incremented inside the inner expansion while loop, we can start the right by incrementing 1 for the next expansion.

The function findLengthOfLCIS returns maxi, denoting the length of the longest continuous increasing subsequence found in nums.

Analysis

Time Complexity: O(N)

• A single pass through the array nums is conducted, with each element being evaluated exactly once to determine its contribution to a continuous increasing subsequence, ensuring linear time complexity.

Space Complexity: O(1)

• Constant space is utilized, as the solution employs only a few variables (left, right, maxi, and prev) to track the progress of the sliding window and record the maximum subsequence length.

Python

def findLengthOfLCIS(self, nums: List[int]) -> int:
    n = len(nums)
    left = right = 0
    maxi = 0
    prev = -1

    while right < n:
        # Expansion
        while right < n and prev < nums[right]:
            prev = nums[right]
            right += 1
        # Logic
        maxi = max(maxi, right - left)
        # Shrinking
        prev = nums[right] if right < n else None
        left = right
        right += 1

    return maxi

1839. Longest Substring Of All Vowels in Order (Medium)

Solution

The task is to find the length of the longest beautiful substring in the given string word. A beautiful substring is defined as one that contains all five vowels (‘a’, ‘e’, ‘i’, ‘o’, ‘u’) in order and without any repetition. This problem can be solved using a sliding window approach, complemented by a set to track the unique vowels encountered within the current window.

The solution iterates through word, adjusting the window to capture sequences that potentially form a beautiful substring. The seen set records the vowels encountered to ensure the substring includes all required vowels in order.

Expansion:

• Expand the window by moving the right pointer forward, adding vowels to the seen set and updating prev to maintain the order condition (i.e., the current character should not precede the previous one in the sequence).

Logic:

• After each expansion, if seen contains all five vowels (indicating a beautiful substring), calculate the current window’s length (right - left) and update maxi if a longer beautiful substring is found.

Shrinking:

• Reset seen to prepare for identifying the next potential beautiful substring. Adjust prev to the current character at right (or None if at the end of word), and set left to start from the current right, moving the window forward.

The function longestBeautifulSubstring returns maxi, denoting the length of the longest beautiful substring found in word.

Analysis

Time Complexity: O(N)

• The algorithm performs a single pass through the string word, with each character being considered for inclusion in the window exactly once. This approach, combined with constant-time operations for adjusting the window and updating seen, ensures linear time complexity.

Space Complexity: O(1)

• Constant space is used, as the solution employs a set to track the vowels within the current window and a few variables to manage the window’s boundaries and record the maximum substring length. The set seen is limited to at most five elements (the vowels), indicating a constant space requirement.

Python

def longestBeautifulSubstring(self, word: str) -> int:
    n = len(word)
    left = right = 0
    seen = set()
    maxi = 0
    prev = word[0]
    while right < n:
        # Expansion
        while right < n and prev <= word[right]:
            prev = word[right]
            seen.add(word[right])
            right += 1
        # Logic
        if len(seen) == 5:
            maxi = max(maxi, right - left)
        # Shrinking
        seen = set()
        prev = word[right] if right < n else None
        left = right
    return maxi

---

Miscellaneous

1208. Get Equal Substrings Within Budget (Medium)

Solution

The problem asks for the maximum length of a non-empty substring of s that can be made equal to the corresponding substring of t, under the condition that the total cost of making all characters of the substring equal does not exceed maxCost. The cost of changing a character to another character is equal to the absolute difference in their ASCII values. This solution employs a sliding window approach, where the window dynamically adjusts to maximize the substring length while keeping the total cost within the budget.

Expansion:

• Expand the window by incrementally including characters from the right, calculating the cost for each new character added to the window. The cost is determined by the absolute difference in ASCII values between corresponding characters in s and t.

Shrinking:

• If the total cost exceeds maxCost, shrink the window from the left by removing characters until the total cost is within the budget again.

Logic:

• After each valid expansion (where the total cost is within the budget) or necessary shrinking (to reduce the total cost), update maxi to capture the maximum length of a valid substring found so far.

The function equalSubstring iterates through the strings s and t, adjusting the window size as described, and returns maxi, representing the length of the longest substring where the total cost of making characters equal does not exceed maxCost.

Analysis

Time Complexity: O(N)

• The solution involves a single pass through the strings s and t with the sliding window, ensuring linear time complexity relative to the length of the strings.

Space Complexity: O(1)

• Constant space is utilized, as the solution employs a minimal number of variables (left, right, diff, maxi) to manage the window’s boundaries and compute the total cost within it. The space required does not scale with the size of the input strings.

Python

def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
    n = len(s)
    left = right = 0
    diff = maxi = 0

    # Function to calculate the cost of making characters at position i equal
    get_diff = lambda i: abs(ord(s[i]) - ord(t[i]))

    while right < n:
        # Expansion: Include the cost of the new character
        diff += get_diff(right)
        right += 1

        # Shrinking: Reduce the window size if total cost exceeds maxCost
        while left < right and diff > maxCost:
            diff -= get_diff(left)
            left += 1

        # Logic: Update the maximum length found
        maxi = max(maxi, right - left)

    return maxi

1658. Minimum Operations to Reduce X to Zero (Medium)

Solution

To find the shortest required operations that sum up to x from both ends is to find the longest subarray that sums up to total - x.

This challenge involves determining the minimum number of operations needed to reduce the sum of all elements in the array nums to a specific target value x. An operation is defined as removing an element from either the beginning or the end of the array. The solution employs a sliding window approach to find the longest subarray whose sum equals sum(nums) - x, which indirectly gives us the smallest number of elements to remove.

The key insight is to invert the problem: instead of directly finding the elements to remove, we identify the largest contiguous subarray with a total sum of sum(nums) - x. The length of the array minus the length of this subarray gives the minimum number of operations required.

Expansion:

• Traverse the array with a sliding window, incrementing total by each element included in the window as the right pointer advances.

Shrinking:

• If the total exceeds needed (the sum required for the subarray), shrink the window from the left by decrementing total with the value of the element at left and incrementing left.

Logic:

• When the total matches needed, update maxi with the maximum length of such a subarray found so far.

If a valid subarray is found (maxi is not zero), the minimum operations required are calculated as the total array length minus the length of this subarray. If no such subarray exists, return -1.

Analysis

Time Complexity: O(N)

• The solution involves a single pass through nums with the sliding window, ensuring linear time complexity as each element is considered exactly once for inclusion and possible removal from the total sum calculation.

Space Complexity: O(1)

• Constant space is required, as the algorithm utilizes a fixed number of variables (left, right, total, maxi) to manage the window and track the sum within it, independent of the size of the input array.

Python

def minOperations(self, nums: List[int], x: int) -> int:
    n = len(nums)
    needed = sum(nums) - x
    if needed == 0:
        return n
    left = right = 0
    total = 0
    maxi = 0
    while right < n:
        # Expansion
        total += nums[right]
        right += 1
        # Shrinking
        while left < right and total > needed:
            total -= nums[left]
            left += 1
        # Logic
        if total == needed:
            maxi = max(maxi, right - left)
    return n - maxi if maxi != 0 else -1

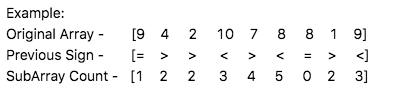
978. Longest Turbulent Subarray (Medium)

Solution

The objective is to find the length of the longest turbulent subarray in a given array arr. A turbulent subarray alternates between elements being strictly greater than and then less than, or vice versa, the adjacent elements. This problem is effectively tackled using a sliding window approach, complemented by a mechanism to dynamically assess the turbulence condition of the current window.

The solution iterates through arr, adjusting the window to encapsulate the longest sequence meeting the turbulent criteria. A helper function is_turbulent is employed to evaluate whether the current window’s expansion maintains the turbulent pattern.

Initialization:

• Start with a window of size 2 (left = 0, right = 1) and assess its turbulence. Handle the case where n == 1 by immediately returning 1.

Expansion:

• Expand the window by moving the right pointer forward, ensuring each subsequent element alternates in comparison (less than or greater than) to the previous element, as dictated by the turbulent pattern.

Logic:

• After each potential expansion, update maxi to capture the maximum length of a turbulent subarray found so far.

Shrinking:

• Prepare for the next potential turbulent subarray by setting left to one position behind right to maintain at least one element in the window that adheres to the turbulence criteria. Reset turbulency to evaluate the turbulence pattern anew. If two consecutive elements are equal, adjust left and right to skip these elements, as they break the turbulent pattern.

The function maxTurbulenceSize returns maxi, indicating the length of the longest turbulent subarray identified in arr.

Analysis

Time Complexity: O(N)

• The solution involves iterating through the array arr once, with each element being evaluated for its contribution to the turbulent subarray. Adjustments to the window are performed in constant time, ensuring linear time complexity.

Space Complexity: O(1)

• Constant space is used, as the algorithm employs a minimal number of variables (left, right, maxi, and turbulency) to manage the window’s boundaries and track the longest turbulent subarray length.

Python

def maxTurbulenceSize(self, arr: List[int]) -> int:
    n = len(arr)
    if n == 1:
        return 1
    left, right = 0, 1
    turbulency = None
    maxi = 0

    def is_turbulent():
        nonlocal turbulency
        if turbulency is None:
            turbulency = "lt" if arr[right - 1] < arr[right] else turbulency
            turbulency = "gt" if arr[right - 1] > arr[right] else turbulency
            return arr[right - 1] != arr[right]
        elif turbulency == "lt":
            turbulency = "gt"
            return arr[right - 1] > arr[right]
        else:
            turbulency = "lt"
            return arr[right - 1] < arr[right]

    while right < n:
        # Expansion
        while right < n and is_turbulent():
            right += 1
        # Logic
        maxi = max(maxi, right - left)
        # Shrinking
        turbulency = None
        left = right - 1
        if right < n and arr[left] == arr[right]:
            left += 1
            right += 1

    return maxi

2401. Longest Nice Subarray (Medium)

Solution

The challenge is to find the length of the longest “nice” subarray within a given array nums. A subarray is considered “nice” if the bitwise OR of all its elements does not contain any overlapping set bits, meaning no two elements share a set bit in the same position. This solution employs a sliding window technique, utilizing bitwise operations to efficiently track the aggregate OR (current_or) of elements within the current window and dynamically adjust the window to maximize its “niceness”.

Expansion:

• Increment the right pointer to include new elements in the window, updating current_or with the bitwise OR of the current elements. The expansion continues until adding another element would cause current_or to have overlapping set bits with the new element.

Logic:

• After each valid expansion, update maxi to capture the maximum length of the “nice” subarray found so far, calculated as right - left.

Shrinking:

• If the next element to be included shares a set bit with current_or (indicating the subarray would no longer be “nice”), shrink the window from the left by removing elements one by one. Adjust current_or by performing a bitwise XOR with the removed element to unset the bits contributed by that element.

The function longestNiceSubarray iterates through nums, adjusting the window size as described, and returns maxi, representing the length of the longest “nice” subarray found.

Analysis

Time Complexity: O(N)

• The solution involves iterating through the array nums once with the sliding window, expanding and shrinking based on the bitwise criteria. Each element is considered exactly once for inclusion in the window, ensuring linear time complexity.

Space Complexity: O(1)

• Constant space is utilized, as the solution employs a minimal number of variables (left, right, current_or, maxi) to manage the window’s boundaries and compute the aggregate bitwise OR within it.

Python

def longestNiceSubarray(self, nums: List[int]) -> int:
    n = len(nums)
    left = right = 0
    current_or = maxi = 0
    while right < n:
        # Expansion
        while right < n and current_or & nums[right] == 0:
            current_or |= nums[right]
            right += 1
        # Logic
        maxi = max(maxi, right - left)
        # Shrinking
        while left < right and right < n and current_or & nums[right] != 0:
            current_or ^= nums[left]
            left += 1
    return maxi