Fixed Window¶

Prospect: https://leetcode.com/problems/sliding-window-median/description/

Naïve Sum/Average¶

while expand

Max Sum Subarray of size K (Easy)¶

Solution

The objective is to find the maximum sum of all contiguous subarrays of length K in a given array. This problem can be efficiently solved by employing the sliding window technique to maintain the sum of elements within the current window, subsequently finding the maximum sum.

Expansion:

Incrementally add each element’s value to a running total as the right pointer advances, until the window reaches the desired size K.
This phase accumulates the initial sum required to compute the first potential maximum sum.

Logic:

Compare the current window’s sum with the maximum sum recorded so far and update the maximum sum if the current window’s sum is greater.

Shrinking:

Before advancing the window, subtract the element at the left edge of the window from the total sum.
Increment the left pointer to slide the window one position to the right, preparing for the next window’s sum calculation.

Analysis

Time Complexity: O(N)

N is the total number of elements in the array.
The algorithm ensures each element is added and subtracted exactly once, resulting in a linear time complexity.

Space Complexity: O(1)

The space complexity is constant as the solution utilizes a fixed number of variables, irrespective of the input array’s size.

def maximumSumSubarray(self, K, Arr, N):
    left = right = 0
    maxi = total = 0
    while right < N:
        # Expansion
        while right < N and right - left < K:
            total += Arr[right]
            right += 1
        # Logic
        maxi = max(maxi, total)
        # Shrinking
        total -= Arr[left]
        left += 1
    return maxi

643. Maximum Average Subarray I (Easy)¶

Solution

The goal is to find the maximum average value of all contiguous subarrays of length k. This can be efficiently solved using the sliding window technique to keep track of the sum of the current window, then calculating its average.

Expansion:

Iterate through the array using a right pointer, adding each element’s value to the total sum until the window reaches size k.
This step builds up the initial sum required to calculate the first average, and in subsequent loop, it will add right element one by one.

Logic:

Calculate the average of the current window by dividing the total sum by k.
Update the maximum average found so far if the current window’s average is higher.

Shrinking:

Before moving the window forward, subtract the element at the left of the window from the total sum.
Increment the left pointer to effectively move the window one position to the right.

Analysis

Time Complexity: O(N)

N is the number of elements in the input array.
Each element is processed exactly once, making the algorithm linear time.

Space Complexity: O(1)

Only a fixed number of variables are used, independent of the input array size.

def findMaxAverage(self, nums: List[int], k: int) -> float:
    n = len(nums)
    left, right = 0, 0
    maxi = -float("inf")  # Since negative numbers are allowed in the array
    total = 0
    while right < n:
        # Expansion
        while right < n and right - left < k:
            total += nums[right]
            right += 1
        # Logic
        maxi = max(maxi, total / k)
        # Shrinking
        total -= nums[left]
        left += 1
    return maxi

1343. Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold (Medium)¶

Solution

The challenge is to compute the count of contiguous subarrays of length k whose average is greater than or equal to a given threshold. This can be efficiently tackled using the sliding window technique, which maintains the sum of the current window’s elements to calculate averages quickly.

Expansion:

Iterate through the array using a right pointer, adding each element’s value to a running total as the right pointer moves, until the window attains the specified size k.
This step accumulates the sum needed to evaluate the first average for comparison against the threshold.

Logic:

threshold_criteria(): Determine if the average of the current window meets or exceeds the threshold. Increment the count (ans) if it does.
The average is computed by dividing the total sum by k and comparing it to the threshold.

Shrinking:

Before advancing the window, subtract the leftmost element’s value from the total sum.
Increment the left pointer to shift the window one position to the right, thereby preparing for the next sum and average computation.

Analysis

Time Complexity: O(N)

N is the total number of elements in the array.
The algorithm ensures each element is processed exactly once, leading to a linear time complexity.

Space Complexity: O(1)

The space complexity is constant as the solution employs a fixed number of variables, regardless of the input array’s size.

def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:
    n = len(arr)
    left = right = 0
    total = ans = 0

    threshold_criteria = lambda: int((total / k) >= threshold)

    while right < n:
        # Expansion
        while right < n and right - left < k:
            total += arr[right]
            right += 1
        # Logic
        ans += threshold_criteria()
        # Shrinking
        total -= arr[left]
        left += 1
    return ans

2090. K Radius Subarray Averages (Medium)¶

Solution

The task is to find the average of all subarrays of length 2 * k + 1 for each center element in the given array, nums, with k elements on both sides. If the subarray cannot be formed due to the lack of elements on either side, the result is -1 for that center.

Expansion:

Traverse the array using a right pointer, adding each element’s value to a cumulative total until the window reaches the size 2 * k + 1.
This step builds up the initial sum required for the first average calculation that meets the window size criterion.

Logic:

Calculate the average of the current window by dividing the total sum by the window size (w) and assign it to the center position of the window.
Utilize lambda functions for calculating the center position and the average to simplify the code.

Shrinking:

Before moving the window forward, subtract the leftmost element’s value from the total sum to prepare for the next window’s average calculation.
Increment the left pointer to effectively shift the window one position to the right.

Analysis

Time Complexity: O(N)

N is the number of elements in the input array.
Each element is processed exactly once, contributing to a linear time complexity overall.

Space Complexity: O(N)

The output array ans has the same length as the input array, nums, dictating a space requirement proportional to the size of the input.

def getAverages(self, nums: List[int], k: int) -> List[int]:
    n = len(nums)
    w = 2 * k + 1  # window size
    ans = [-1] * n
    if w > n:  # If window size is more than the array length
        return ans

    center = lambda: left + (right - left) // 2
    average = lambda: total // w

    left = right = 0
    total = 0
    while right < n:
        # Expansion
        while right < n and right - left < w:
            total += nums[right]
            right += 1
        # Logic
        ans[center()] = average()
        # Shrinking
        total -= nums[left]
        left += 1
    return ans

1423. Maximum Points You Can Obtain from Cards (Medium)¶

Solution

An alternative viewpoint for solving this problem involves minimizing the sum of the remaining cards after choosing k cards from either the beginning or the end of the array. Essentially, we find the minimum sum of a subarray of length n - k (where n is the total number of cards), as the complement to maximizing the points from the chosen cards.

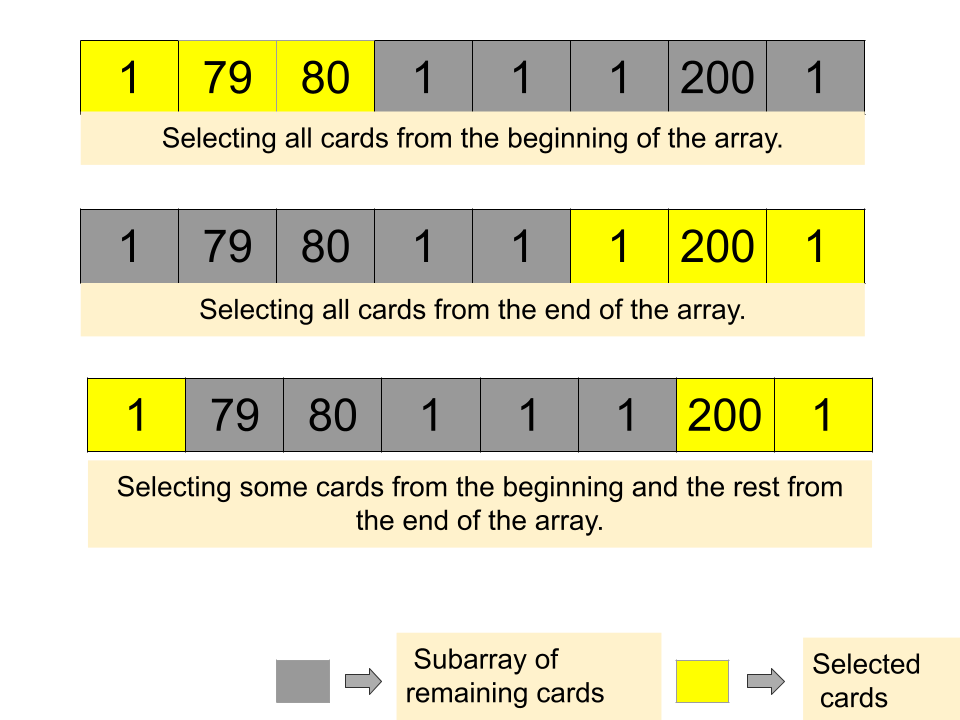
../../../_images/sliding-window-maximum-points-you-obtain-from-cards.png

Expansion:

Progress through the array with a right pointer, adding each card’s points to a cumulative total until the window reaches the size n - k.
This phase accumulates the initial sum for the potential minimum subarray.

Logic:

Update the minimum sum encountered so far with the total of the current window.
The objective is to identify the smallest possible sum for any window of size n - k within the card points array.

Shrinking:

Before advancing the window, subtract the leftmost card’s points from the total sum.
Increment the left pointer to shift the window one position to the right, preparing for the next window’s sum evaluation.

The final score is calculated by subtracting this minimum sum from the total sum of all card points, effectively maximizing the points obtained from the chosen cards.

Analysis

Time Complexity: O(N)

N is the total number of cards.
The algorithm ensures each card is added and subtracted from the total sum exactly once, leading to a linear time complexity.

Space Complexity: O(1)

The space complexity is constant as the solution uses a fixed number of variables, independent of the number of cards.

def maxScore(self, cardPoints: List[int], k: int) -> int:
    n = len(cardPoints)
    w = n - k  # We need to minimize sum of window with size n-k
    arr_total = sum(cardPoints)
    if k == n:
        return arr_total

    left = right = 0
    total = 0
    mini = float("inf")
    while right < n:
        # Expansion
        while right < n and right - left < w:
            total += cardPoints[right]
            right += 1
        # Logic
        mini = min(mini, total)
        # Shrinking
        total -= cardPoints[left]
        left += 1

    return arr_total - mini

1176. Diet Plan Performance (Easy)¶

Solution

The objective is to calculate a diet plan’s performance score based on daily calorie intake. The score increments by 1 if the total calories of a contiguous subarray of length k exceed the upper limit, decrements by 1 if they fall below the lower limit, and remains unchanged otherwise.

Expansion:

Iterate through the calories array with a right pointer, summing up the calories until reaching a subarray of length k.
This step accumulates the calories for the initial evaluation of the diet plan’s performance within the specified window.

Logic:

Apply a lambda function, performance, to determine the score adjustment based on the total calories in the current window relative to the upper and lower limits.
Increment or decrement the overall score (ans) according to the performance of the current window.

Shrinking:

Before advancing the window, subtract the leftmost calorie count from the total sum to prepare for the next window’s evaluation.
Increment the left pointer to shift the window one position to the right, ensuring continuous assessment of the diet plan’s performance across the array.

The final performance score is obtained by aggregating the adjustments (increments or decrements) for all valid windows of length k throughout the array.

Analysis

Time Complexity: O(N)

N is the total number of days (or the length of the calories array).
Each day’s calorie count is processed exactly once, contributing to a linear time complexity.

Space Complexity: O(1)

The space complexity is constant as the solution uses a fixed number of variables, regardless of the diet plan’s duration.

def dietPlanPerformance(
    self, calories: List[int], k: int, lower: int, upper: int
) -> int:
    n = len(calories)
    left = right = 0
    total = ans = 0

    performance = lambda: -1 if total < lower else int(total > upper)

    while right < n:
        # Expansion
        while right < n and right - left < k:
            total += calories[right]
            right += 1
        # Logic
        ans += performance()
        # Shrinking
        total -= calories[left]
        left += 1

    return ans

1052. Grumpy Bookstore Owner (Medium)¶

Solution

The task is to maximize the number of satisfied customers in a bookstore by choosing a minutes long interval to make the grumpy owner act normally. The arrays customers and grumpy indicate the number of customers in each minute and whether the owner is grumpy (1) or not (0), respectively.

The strategy involves finding the maximum number of customers that can be satisfied during the owner’s grumpy period by utilizing the minutes interval effectively. The solution uses a sliding window approach to calculate this:

Expansion:

Traverse the customers array, adding to grumpy_total the number of customers that would be unsatisfied due to the owner’s grumpiness within the window of size minutes.
This phase aims to identify the interval where making the owner not grumpy would result in the maximum number of additional satisfied customers.

Logic:

Update maxi to keep track of the maximum number of customers that can be satisfied by utilizing the minutes interval optimally.
This involves comparing the current grumpy_total with maxi and updating maxi if grumpy_total is greater.

Shrinking:

Before moving the window forward, check if the leftmost minute involved the grumpy owner. If so, subtract those customers from grumpy_total.
Increment the left pointer to shift the window one position to the right, ensuring the window size remains constant as it moves across the array.

The final count of satisfied customers is the sum of customers already satisfied (when the owner is not grumpy) and the maximum additional customers that can be satisfied during the owner’s grumpy period.

Analysis

Time Complexity: O(N)

N is the total number of minutes (or the length of the customers and grumpy arrays).
The algorithm iterates through each minute exactly once, leading to a linear time complexity.

Space Complexity: O(1)

The space complexity is constant as the solution employs a fixed number of variables, regardless of the input size.

def maxSatisfied(self, customers: List[int], grumpy: List[int], minutes: int) -> int:
    n = len(customers)
    left = right = 0
    # Calculate already satisfied customers, ignoring grumpy periods
    already_satisfied = sum(i * (not j) for i, j in zip(customers, grumpy))
    grumpy_total = maxi = 0

    while right < n:
        # Expansion: Add customers affected by grumpiness within the window
        while right < n and right - left < minutes:
            if grumpy[right] == 1:
                grumpy_total += customers[right]
            right += 1
        # Logic: Update maxi if the current window has more grumpy-affected customers
        maxi = max(maxi, grumpy_total)
        # Shrinking: Remove the leftmost customer count if it was during a grumpy period
        if grumpy[left] == 1:
            grumpy_total -= customers[left]
        left += 1
    # Return the sum of always satisfied customers and the maximum recoverable during grumpy periods
    return maxi + already_satisfied

1652. Defuse the Bomb (Easy)¶

Solution

This problem involves decrypting a given code by replacing each element with the sum of the next k elements. If k is negative, the sum involves the previous k elements. A special case occurs when k is zero, resulting in all elements being replaced by zero. The solution employs a sliding window approach, adjusted to handle both positive and negative k values, as well as the circular nature of the code array.

To accommodate the circular array and the direction specified by k, a helper lambda function get_index is used to determine the correct index for assignment in the ans array based on the direction of summation.

Expansion:

Progress through the code array (considered circularly due to modulo operation), summing up to k elements ahead (or behind, for negative k) as specified.

Logic:

Assign the computed total to the appropriate position in the ans array, determined by the current window’s bounds and the direction indicated by k.

Shrinking:

Before advancing the window, subtract the value of the element exiting the window from the total, ensuring the sum remains accurate for the window’s current position.

The function returns ans, the decrypted code, after processing the entire array.

Analysis

Time Complexity: O(N + K)

The algorithm iterates through the array potentially more than once due to the nature of the circular array and the need to sum k elements for each position, where N is the length of the code array and K is the absolute value of the given k.

Space Complexity: O(N)

A new array ans of the same length as code is created to store the decrypted code, dictating a space requirement linearly proportional to the size of the input array.

def decrypt(self, code: List[int], k: int) -> List[int]:
    n = len(code)
    negative = k < 0
    k = -k if negative else k
    left = right = 0
    total = 0
    ans = [0] * n

    get_index = lambda: right % n if negative else (left - 1) % n

    while right < (n + k - 1):
        # Expansion
        while right < (n + k - 1) and right - left < k:
            total += code[right % n]
            right += 1
        # Logic
        ans[get_index()] = total
        # Shrinking
        total -= code[left % n]
        left += 1
    return ans

Hashmap¶

while expand

187. Repeated DNA Sequences (Medium)¶

Solution

This problem aims to identify all DNA sequences of length 10 that appear more than once in a given string s. A sliding window combined with a frequency counter approach is employed to efficiently find and record these repeated sequences.

The solution iterates through s, maintaining a window of exactly 10 characters and using a counter to track the occurrence of each unique sequence within this window size. When a sequence’s count reaches 2 (indicating a repeat), it is added to the answer list.

Expansion:

Increment the right pointer to expand the window until it encompasses 10 characters, corresponding to the required sequence length.

Logic:

After forming a window of size 10, check the occurrence of the current sequence. If it’s the second time the sequence has appeared, add it to ans.

Shrinking:

Increment the left pointer by 1 for each iteration to move the window forward and examine the next sequence.

The function findRepeatedDnaSequences returns ans, a list containing all sequences that are repeated in the DNA string.

Analysis

Time Complexity: O(N)

The algorithm performs a single pass through the string s, examining each possible 10-character sequence once. While the window size remains constant, the sliding operation ensures linear time complexity.

Space Complexity: O(N)

Space complexity is primarily influenced by the storage required for the counter and the ans list.

def findRepeatedDnaSequences(self, s: str) -> List[str]:
    n = len(s)
    k = 10
    left = right = 0
    counter = collections.Counter()
    ans = []
    while right < n:
        # Expansion
        while right < n and right - left < k:
            right += 1
        # Logic
        if right - left == k:
            sub = s[left:right]
            counter[sub] += 1
            # Add the sequence to ans the second time it occurs
            if counter[sub] == 2:
                ans.append(sub)
        # Shrinking
        left += 1
    return ans

Hashmap - Duplicate Elements¶

while expand

Generic Solution: Find Duplicates within Window Size `k`¶

Solution

The objective is to determine whether an array contains any duplicate elements within a window of size k. This problem can be efficiently solved by using a sliding window technique coupled with a hashmap (counter) to keep track of element frequencies within the current window.

Expansion:

Progress through the array using a right pointer, updating the hashmap with the count of each element encountered. This allows for tracking the frequency of elements within the window.
The window expands until it reaches the maximum allowed size of k.

Logic:

A lambda function, has_duplicates, checks if the current window contains any duplicates by comparing the window’s size to the number of unique elements (dictated by the hashmap’s size). If these sizes do not match, a duplicate exists within the window.
If duplicates are found, the function returns True.

Shrinking:

Before moving the window forward, decrement the count of the leftmost element in the hashmap and remove it from the hashmap if its count reaches zero. This step effectively shrinks the window from the left, preparing for the next iteration.
Increment the left pointer to shift the window one position to the right, ensuring the window size is maintained as it moves through the array.

The function returns False if no duplicates are found within any window of size k throughout the array. This approach provides a dynamic check for duplicates within a moving window across the array.

Analysis

Time Complexity: O(N)

N is the total number of elements in the array.
The algorithm iterates through each element at most twice (once when adding to the hashmap and once when removing), leading to a linear time complexity.

Space Complexity: O(k)

The hashmap may store up to k distinct elements, where k is the size of the window. Hence, the space complexity is proportional to the size of the window.

def containsDuplicatesInK(self, arr: List[int], k: int) -> bool:
    n = len(arr)
    left = right = 0
    counter = {}

    has_duplicates = lambda: right - left != len(counter)

    while right < n:
        # Expansion
        while right < n and right - left < k:
            counter[arr[right]] = counter.get(arr[right], 0) + 1
            right += 1
        # Logic
        if has_duplicates():
            return True
        # Shrinking
        counter[arr[left]] -= 1
        if counter[arr[left]] == 0:
            counter.pop(arr[left])
        left += 1
    return False

219. Contains Duplicate II (Easy)¶

Solution

The problem asks whether there are any duplicates in an array such that the two indices i and j of the same value satisfy abs(i - j) <= k. This can be viewed as a specific instance of finding duplicates within a window of size k, which aligns with our generic solution.

We leverage the generic solution containsDuplicatesInK, which checks for duplicates within a window size. However, due to the inclusive nature of the condition (abs(i - j) <= k), we adjust the window size to k + 1 to accurately capture the requirement.

By simply passing the input array nums and the adjusted window size to containsDuplicatesInK, we can efficiently determine the presence of such duplicates.

Analysis

Time Complexity: O(N)

N is the number of elements in the input array nums.
The algorithm iterates through the array once, maintaining a dynamic window of size k + 1 to check for duplicates.

Space Complexity: O(k)

The space complexity is proportional to the size of the window, which holds up to k + 1 elements at any time. Hence, the space requirement depends on the value of k.

def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
    k = k + 1  # since there is an '=' in abs(i - j) <= k
    return self.containsDuplicatesInK(nums, k)

217. Contains Duplicate (Easy)¶

Solution

This problem asks whether any value appears at least twice in the array, which is a simpler variant of detecting duplicates without the constraint of a fixed window size. We can utilize the generic solution containsDuplicatesInK, designed for finding duplicates within a specified window, by considering the entire array as a single window.

To adapt the generic solution to this problem, we set the window size k to the length of the array. This effectively checks for any duplicates across the whole array, meeting the problem’s requirement.

Analysis

Time Complexity: O(N)

N is the number of elements in the input array nums.
The algorithm iterates through the array once with the help of the generic solution, efficiently checking for any duplicates.

Space Complexity: O(N)

The space complexity depends on the number of unique elements stored in the hashmap, which, in the worst case, could be all the elements in the array.

def containsDuplicate(self, nums: List[int]) -> bool:
    k = len(nums)  # since entire array is considered
    return self.containsDuplicatesInK(nums, k)

Hashmap - Unique/Distinct Elements¶

while expand

1876. Substrings of Size Three with Distinct Characters (Easy)¶

Solution

The goal is to identify and count all substrings of length three that contain distinct characters in a given string. A sliding window approach, augmented with a hashmap to track the frequency of characters within the window, elegantly solves this problem.

Expansion:

Traverse the string s with a sliding window of size three (k = 3), using a right pointer to add characters to the hashmap and keeping count of their frequencies.
This ensures we consider only substrings of the exact length for distinctiveness.

Logic:

A lambda function, is_distinct, checks if the window (substring) has all distinct characters by comparing the size of the hashmap (unique characters) with k.
If the substring meets the criteria, increment the count (ans).

Shrinking:

Before shifting the window rightward, decrease the count of the leftmost character and remove it from the hashmap if its frequency drops to zero.
This step maintains the window’s size by adjusting its left boundary.

The total count of such “good” substrings is returned, quantifying substrings of size three with unique characters.

Analysis

Time Complexity: O(N)

The algorithm processes each character in the string s a fixed number of times (at most twice), leading to linear time complexity.

Space Complexity: O(1)

The hashmap’s size is constrained by the window size (k = 3), ensuring a constant space requirement irrespective of the string’s length.

def countGoodSubstrings(self, s: str) -> int:
    n = len(s)
    k = 3  # Fixed window size for substrings of length three
    left = right = 0
    counter = {}  # To track frequencies of characters in the current window
    ans = 0  # To count substrings with distinct characters

    # Lambda function to check if the window has distinct characters
    is_distinct = lambda: len(counter) == k

    while right < n:
        # Expansion: Update the character frequency in the window
        while right < n and right - left < k:
            counter[s[right]] = counter.get(s[right], 0) + 1
            right += 1
        # Logic: If all characters in the window are distinct, increment ans
        ans += is_distinct()
        # Shrinking: Move the window forward by adjusting character frequencies
        counter[s[left]] -= 1
        if counter[s[left]] == 0:  # Remove character from hashmap if its count is zero
            counter.pop(s[left])
        left += 1
    return ans

1852. Distinct Numbers in Each Subarray (Medium)¶

Also

Count distinct elements in every window (Easy)

Solution

This problem requires calculating the number of distinct integers in every subarray of size k within a given array. The solution employs a sliding window technique alongside a hashmap to efficiently track the frequency of elements and thus the distinctness within each window.

Expansion:

Iterate through the array nums with a sliding window of size k, incrementing the frequency of each element in the hashmap as the window expands.
This step ensures that all elements within the current window are accounted for in terms of frequency.

Logic:

Upon reaching a window of size k, record the number of unique elements by appending the size of the hashmap to the ans list. This size reflects the count of distinct numbers in the window.
The operation captures the essence of the problem by focusing on the distinctness of elements within each subarray of the specified size.

Shrinking:

Before moving the window forward, decrement the frequency of the element exiting the window (leftmost element) and remove it from the hashmap if its frequency reaches zero.
This step adjusts the window’s left boundary while maintaining its size and ensuring that only elements within the current window are considered for distinctness.

The final result is a list (ans) containing the count of distinct numbers for each subarray of size k across the entire array.

Analysis

Time Complexity: O(N)

The algorithm iterates through the array once, processing each element a fixed number of times (once when entering and once when leaving the window), thereby achieving linear time complexity.

Space Complexity: O(k)

The space complexity primarily depends on the hashmap, which at most contains k distinct elements at any given time, where k is the size of the window.

def distinctNumbers(self, nums: List[int], k: int) -> List[int]:
    n = len(nums)
    left = right = 0
    counter = {}
    ans = []
    while right < n:
        # Expansion
        while right < n and right - left < k:
            counter[nums[right]] = counter.get(nums[right], 0) + 1
            right += 1
        # Logic
        ans.append(len(counter))
        # Shrinking
        counter[nums[left]] -= 1
        if counter[nums[left]] == 0:
            counter.pop(nums[left])
        left += 1
    return ans

2107. Number of Unique Flavors After Sharing K Candies (Medium)¶

Solution

This problem involves determining the maximum number of unique candy flavors one can have after giving away exactly k candies. The solution uses a sliding window approach combined with a counter to track the frequency of each candy flavor as the window slides through the array of candies.

The main idea is to simulate the process of removing candies from the collection (to share) and then to calculate the number of unique flavors remaining. The window size effectively represents the number of candies being shared at any given time, and the counter tracks the diversity of the remaining collection.

Initial Check:

If k is 0, sharing does not occur, so the total unique flavors are returned immediately, determined by the length of the counter.

Expansion:

Traverse the candies array, decrementing the count for each candy flavor as it enters the window. If a candy’s count drops to zero, it’s removed from the counter, simulating the sharing of that candy.
This process continues until k candies have been considered for sharing.

Logic:

After each sharing session (or upon reaching a window of size k), update maxi with the maximum between its current value and the number of unique flavors currently in the counter.
This step ensures we capture the highest diversity of flavors after any sharing session.

Shrinking:

Increment the left boundary of the window to simulate the end of a sharing session and the potential start of a new one. The count of the leftmost candy is incremented, effectively returning it to the collection.
Continue this process until the end of the candies array is reached, ensuring every possible sharing scenario is evaluated.

The solution returns maxi, the maximum number of unique flavors that can be achieved after sharing k candies.

Analysis

Time Complexity: O(N)

Iterating through the candies array once and modifying the counter for each candy ensures linear time complexity.

Space Complexity: O(N)

The counter may initially contain every candy flavor, so its size is proportional to the number of unique candy flavors, which can be as large as the input array itself.

def shareCandies(self, candies: List[int], k: int) -> int:
    n = len(candies)
    counter = collections.Counter(candies)
    if k == 0:
        return len(counter)
    left = right = 0
    maxi = 0
    while right < n:
        # Expansion
        while right < n and right - left < k:
            counter[candies[right]] -= 1
            if counter[candies[right]] == 0:
                counter.pop(candies[right])
            right += 1
        # Logic
        maxi = max(maxi, len(counter))
        # Shrinking
        counter[candies[left]] = counter.get(candies[left], 0) + 1
        left += 1
    return maxi

1100. Find K-Length Substrings With No Repeated Characters (Medium)¶

Solution

The aim is to count all k-length substrings of a given string s that consist entirely of unique characters. This is achieved using a sliding window and a counter to monitor the frequency of characters within each potential substring.

The process iterates over the string, expanding and shrinking a window of size k, and utilizes a hashmap (counter) to track the occurrences of each character within the window. A substring is deemed valid if it contains no repeated characters, which is determined when the size of the counter (unique characters) matches the window size (k).

Expansion:

Advance through the string with a right pointer, adding characters to the counter, until the window reaches size k. This captures a potential k-length substring for evaluation.

Logic:

Use a lambda function, is_distinct, to assess if the current window forms a valid substring by checking if the count of unique characters equals k.
If the substring is valid (all characters are distinct), increment the answer (ans).

Shrinking:

Before sliding the window to the next position, decrement the count of the character exiting the window (leftmost character) and remove it from the counter if its count drops to zero.
This action maintains the integrity of the counter, ensuring it only reflects the composition of the current window.

The result, ans, represents the total number of k-length substrings within s that are composed of distinct characters.

Analysis

Time Complexity: O(N)

The algorithm iterates through each character in the string once, adjusting the counter as the window expands and shrinks, which achieves linear time complexity.

Space Complexity: O(k)

The space required by the counter is dependent on the number of unique characters within a window of size k. In the worst case, this is equal to k, suggesting the space complexity is proportional to k.

def numKLenSubstrNoRepeats(self, s: str, k: int) -> int:
    n = len(s)
    left = right = 0
    counter = {}
    ans = 0

    is_distinct = lambda: len(counter) == k

    while right < n:
        # Expansion
        while right < n and right - left < k:
            counter[s[right]] = counter.get(s[right], 0) + 1
            right += 1
        # Logic
        ans += is_distinct()
        # Shrinking
        counter[s[left]] -= 1
        if counter[s[left]] == 0:
            counter.pop(s[left])
        left += 1
    return ans

Substrings of length k with k-1 distinct elements (Medium)¶

Solution

The challenge is to count all substrings of length K within a given string S that contain exactly K - 1 distinct characters. This task can be efficiently tackled using a sliding window approach coupled with a hashmap to track the frequency of characters within each window.

The key is to iterate over the string with a window of size K, using the hashmap to count occurrences of each character. A valid substring is one where the total number of distinct characters is exactly K - 1, which implies that exactly one character is repeated once within the window.

Expansion:

Move through the string with a right pointer, incrementing the character counts in the hashmap until the window size reaches K.

Logic:

Determine if the current window forms a valid substring by checking if the number of unique characters (len(counter)) equals K - 1. If so, increment the answer (ans).

Shrinking:

Before shifting the window forward, decrease the count of the leftmost character in the hashmap. If a character’s count drops to zero, remove it from the hashmap.
This step ensures that the hashmap accurately reflects the composition of the current window by excluding the character that just left the window.

The function returns ans, the total count of substrings that meet the criteria.

Analysis

Time Complexity: O(N)

The algorithm sweeps through the string once, with each character being added to and removed from the hashmap no more than once, leading to a linear time complexity.

Space Complexity: O(K)

The space used by the hashmap depends on the window size K, as it holds the counts of characters within the window. In the worst-case scenario, the hashmap could hold up to K different characters, though typically fewer due to the requirement for K - 1 distinct elements.

def countOfSubstrings(self, S, K):
    n = len(S)
    left = right = 0
    counter = {}
    ans = 0
    while right < n:
        # Expansion
        while right < n and right - left < K:
            counter[S[right]] = counter.get(S[right], 0) + 1
            right += 1
        # Logic
        ans += int(len(counter) == K - 1)
        # Shrinking
        counter[S[left]] -= 1
        if counter[S[left]] == 0:
            counter.pop(S[left])
        left += 1
    return ans

Hashmap - Anagrams/Permutations¶

while expand

438. Find All Anagrams in a String (Medium)¶

Solution

This solution employs a hashmap to keep track of the character frequencies in the substring p and compares it with sliding windows of equal length in s. The goal is to find all start indices of p’s anagrams in s.

A hashmap check_counter is initialized with the character counts of p, and another hashmap counter is used to track character frequencies within each window in s. A sliding window expands to the size of p (k), and at each step, the window is checked for an anagram by comparing the two hashmaps.

Expansion:

Increment character counts in counter as the window expands to include new characters from s.

Logic:

Use a lambda function, is_anagram, to check if counter matches check_counter. If so, the current window is an anagram, and the start index is added to ans.

Shrinking:

After checking, decrement the count of the character leaving the window and remove it from counter if its count drops to zero.

Analysis

Time Complexity: O(N)

Processing each character in s involves updating the hashmap, allowing for efficient comparison with the hashmap of p.

Space Complexity: O(1)

The space used by the hashmaps is constrained by the number of distinct characters, which is constant for the alphabet.

def findAnagrams(self, s: str, p: str) -> List[int]:
    n = len(s)
    k = len(p)
    left = right = 0
    check_counter = collections.Counter(p)
    counter = {}
    ans = []

    is_anagram = lambda: counter == check_counter

    while right < n:
        # Expansion
        while right < n and right - left < k:
            counter[s[right]] = counter.get(s[right], 0) + 1
            right += 1
        # Logic
        if is_anagram():
            ans.append(left)
        # Shrinking
        counter[s[left]] -= 1
        if counter[s[left]] == 0:
            counter.pop(s[left])
        left += 1
    return ans

Solution

This solution optimizes the first by using fixed-size arrays to track character frequencies, assuming the input string contains only lowercase alphabets. Each character’s frequency in p and within sliding windows of s is tracked using arrays check_counter and counter, respectively.

A helper function, arr_pos, converts characters to array indices. The arrays are then compared to determine if a window in s is an anagram of p.

Expansion:

Update counter to include character counts as the window expands.

Logic:

The lambda function is_anagram checks if the current window’s character frequency array matches p’s. If the arrays are equal, the window is an anagram, and its starting index is recorded.

Shrinking:

Adjust counter for the character exiting the window, ensuring it accurately reflects the current window’s composition.

Analysis

Time Complexity: O(N)

The algorithm iterates through s once, with efficient array operations to track and compare character frequencies.

Space Complexity: O(1)

The arrays check_counter and counter have fixed sizes based on the alphabet, leading to constant space usage.

def findAnagrams(self, s: str, p: str) -> List[int]:
    n = len(s)
    k = len(p)
    left = right = 0
    check_counter = [0] * 26
    counter = [0] * 26
    ans = []

    arr_pos = lambda i: ord(i) - ord("a")
    is_anagram = lambda: counter == check_counter

    for i in p:
        check_counter[arr_pos(i)] += 1

    while right < n:
        # Expansion
        while right < n and right - left < k:
            counter[arr_pos(s[right])] += 1
            right += 1
        # Logic
        if is_anagram():
            ans.append(left)
        # Shrinking
        counter[arr_pos(s[left])] -= 1
        left += 1
    return ans

242. Valid Anagram (Easy)¶

Solution

To determine if one string is an anagram of another, we can adapt the findAnagrams function, originally designed to find all anagram substrings of p within s. For two strings s and t to be anagrams, s must contain an anagram of t that spans its entire length, and vice versa.

The solution involves a simple check to ensure s and t are of equal length (a prerequisite for anagrams) and then utilizes findAnagrams to search for t within s. If t is a valid anagram of s, findAnagrams should return a non-empty list, indicating the presence of an anagram that covers the entirety of s.

Implementation:

First, verify that s and t have the same length, as differing lengths immediately disqualify them as anagrams.
Use findAnagrams(s, t) to search for anagrams of t within s. For t to be an anagram of s, there must be at least one matching anagram covering the full length of s.

The function returns True if such an anagram exists, indicating s and t are valid anagrams of each other.

Analysis

Time Complexity: O(N)

Leveraging findAnagrams involves scanning through s with a sliding window to match t’s character frequency, leading to linear time complexity based on the length of s.

Space Complexity: O(1)

The space complexity remains constant, determined by the fixed-size data structures used to track character frequencies in the implementation of findAnagrams.

def isAnagram(self, s: str, t: str) -> bool:
    return len(s) == len(t) and self.findAnagrams(s, t) == [0]

567. Permutation in String (Medium)¶

Solution

The objective is to determine if one string s1 is a permutation of any substring in another string s2. This is effectively searching for an anagram of s1 within s2, a problem directly addressed by the findAnagrams function. The function checks for the existence of substrings within s2 that are anagrams of s1, matching the exact character frequencies.

Implementation:

Utilize findAnagrams(s2, s1) to search s2 for any substrings that are anagrams of s1. The function returns a list of starting indices for these anagrams within s2.
The presence of at least one anagram of s1 within s2 (indicated by a non-empty return value) confirms that s1 is a permutation of a substring in s2.

The function returns True if s2 contains a substring that is a permutation of s1, fulfilling the problem’s requirement.

Analysis

Time Complexity: O(N)

The findAnagrams function iterates through s2, examining potential substrings against the character frequency of s1, which scales linearly with the length of s2.

Space Complexity: O(1)

The space complexity is constant, determined by the fixed-size structures used for character frequency tracking in findAnagrams.

def checkInclusion(self, s1: str, s2: str) -> bool:
    return self.findAnagrams(s2, s1) != []

Count¶

while expand

2379. Minimum Recolors to Get K Consecutive Black Blocks (Easy)¶

Solution

The challenge is to determine the minimum number of white blocks (‘W’) that need to be recolored black (‘B’) to achieve a sequence of k consecutive black blocks within the given string blocks. This problem can be efficiently solved using a sliding window approach, tracking the count of white blocks within each window of size k.

The solution iterates through blocks with a window of fixed size k, maintaining a count of white blocks (whites) within the current window. The goal is to find the window with the fewest white blocks, as this represents the minimum recolors needed.

Expansion:

Traverse the string with a right pointer, incrementing the whites count for each white block encountered until the window encompasses k blocks.

Logic:

After each window expansion, update mini to hold the minimum white block count observed in any window thus far. This count represents the least number of recolors required.

Shrinking:

Before sliding the window forward, decrement the whites count if the character leaving the window is a white block. This action effectively moves the window one position to the right, maintaining its size.

The function returns mini, indicating the minimum number of recolors required to obtain k consecutive black blocks in the string.

Analysis

Time Complexity: O(N)

The algorithm requires a single pass through blocks, with each block being added to and then removed from the count of whites within the window, ensuring linear time complexity.

Space Complexity: O(1)

Constant space is utilized, with a limited number of variables needed to track the current window’s state and the running minimum of white blocks.

def minimumRecolors(self, blocks: str, k: int) -> int:
    n = len(blocks)
    left = right = 0
    whites = 0
    mini = n

    is_white = lambda i: int(blocks[i] == "W")

    while right < n:
        # Expansion
        while right < n and right - left < k:
            whites += is_white(right)
            right += 1
        # Logic
        mini = min(mini, whites)
        # Shrinking
        whites -= is_white(left)
        left += 1
    return mini

1456. Maximum Number of Vowels in a Substring of Given Length (Medium)¶

Solution

This problem aims to find the maximum number of vowels in any substring of length k within the given string s. A sliding window approach, complemented by a vowel set for easy identification, efficiently solves this challenge.

The solution iterates through s with a fixed-size window, counting vowels within each potential substring and tracking the maximum count found.

Expansion:

Traverse s with a right pointer, incrementing the vowel count for each character within the window that is identified as a vowel until the window reaches the size k.

Logic:

After each window expansion, update maxi to hold the maximum vowel count observed in any window thus far.

Shrinking:

Before sliding the window rightward, decrement the vowel count if the character leaving the window is a vowel. This ensures the count reflects the current window’s composition accurately.

The function returns maxi, representing the highest number of vowels found in any substring of length k throughout s.

Analysis

Time Complexity: O(N)

The algorithm requires a single pass through s, with operations within each window performed in constant time, resulting in linear time complexity.

Space Complexity: O(1)

The space complexity is constant, attributed to the fixed-size set for vowels and a limited number of variables tracking the current window’s state and the maximum count.

def maxVowels(self, s: str, k: int) -> int:
    n = len(s)
    left = right = 0
    maxi = count = 0

    vowels = set("aeiou")
    is_vowel = lambda i: s[i] in vowels

    while right < n:
        # Expansion
        while right < n and right - left < k:
            count += is_vowel(right)
            right += 1
        # Logic
        maxi = max(maxi, count)
        # Shrinking
        count -= is_vowel(left)
        left += 1
    return maxi

Count - Math¶

while expand

1550. Three Consecutive Odds (Easy)¶

Solution

The challenge is to determine if the array arr contains at least one instance of three consecutive odd numbers. This can be efficiently addressed using a sliding window approach, with a window size of 3, to check for sequences of three consecutive odd numbers within the array.

The solution iterates through arr with a window of fixed size k (3), maintaining a count of odd numbers (odds) within the current window.

Expansion:

Traverse the array with a right pointer, incrementing the odds count for each odd number encountered until the window encompasses k elements.

Logic:

If the count of odd numbers within the window equals k, a sequence of three consecutive odd numbers has been found, and the function returns True.

Shrinking:

Before moving the window forward, decrement the odds count if the leftmost number is odd, effectively shrinking the window from the left while maintaining its size as it slides through the array.

If the function iterates through the entire array without finding three consecutive odd numbers, it returns False.

Analysis

Time Complexity: O(N)

The algorithm sweeps through the array once, with each element being added to and then removed from the count of odds within the window, ensuring linear time complexity.

Space Complexity: O(1)

Constant space is used, as only a fixed number of variables are needed to track the current window’s status and the count of odd numbers.

def threeConsecutiveOdds(self, arr: List[int]) -> bool:
    n = len(arr)
    k = 3
    left = right = 0
    odds = 0

    is_odd = lambda i: arr[i] % 2
    while right < n:
        # Expansion
        while right < n and right - left < k:
            odds += is_odd(right)
            right += 1
        # Logic
        if odds == k:
            return True
        # Shrinking
        odds -= is_odd(left)
        left += 1
    return False

2269. Find the K-Beauty of a Number (Easy)¶

Solution

The task is to count how many substrings of length k within the given number num are divisors of num itself. This problem is addressed using a sliding window approach, where the window of size k slides across the digits of num, converted into an array of integers for easier manipulation.

The solution iterates through the digit array, forming substrings (or sub-numbers) of length k and checking each for divisibility against num. A count (ans) is maintained to track the number of valid divisors found.

Expansion:

Advance through the array with a right pointer, forming sub-numbers by appending digits until reaching the specified length k.

Logic:

Utilize a lambda function, is_divisible, to check if the current sub-number is a non-zero divisor of num, incrementing ans for each valid divisor.

Shrinking:

Before shifting the window forward, remove the leftmost digit from the sub-number to maintain the window size. This is achieved by modulo operation with 10 ^ (k - 1), effectively preparing for the next sub-number’s formation.

The function returns ans, the total count of k-beauty divisors within num.

Analysis

Time Complexity: O(N)

Iterating through the digit array of num involves examining each digit sequence of length k once, leading to linear time complexity relative to the number of digits in num.

Space Complexity: O(N)

Converting num into an array of its digits requires space proportional to the length of num.

def divisorSubstrings(self, num: int, k: int) -> int:
    nums = list(map(int, str(num)))
    n = len(nums)
    left = right = 0
    ans = sub_num = 0

    is_divisible = lambda: int(num) % sub_num == 0 if sub_num != 0 else 0

    while right < n:
        # Expansion
        while right < n and right - left < k:
            sub_num = sub_num * 10 + nums[right]
            right += 1
        # Logic
        ans += is_divisible()
        # Shrinking
        sub_num = sub_num % (10 ** (k - 1))
        left += 1
    return ans

Count - Swaps¶

while expand

1151. Minimum Swaps to Group All 1’s Together (Medium)¶

Solution

This problem requires finding the minimum number of swaps needed to group all 1’s in the array data together. It can be cleverly solved using a sliding window approach, focusing on minimizing the number of zeros within any window of size equal to the total count of 1’s in data.

The key insight is that the minimum number of swaps corresponds to the window with the fewest zeros since each zero represents a swap needed to replace it with a 1 from outside the window.

Initial Check:

If there are no 1’s in data, no swaps are needed, and the function returns 0.

Expansion:

Advance through the array, increasing the count of zeros within the current window until it reaches the size k, which is the total number of 1’s in data.

Logic:

Calculate the minimum number of zeros encountered in any window of size k. This directly translates to the minimum number of swaps required.

Shrinking:

Before moving the window forward, subtract the leftmost value from the zeros count if it’s a zero. This action effectively shrinks the window from the left while maintaining its size as it slides through the array.

The solution returns mini, representing the minimum number of swaps required to group all 1’s together in data.

Analysis

Time Complexity: O(N)

The algorithm iterates through the array once, adjusting the count of zeros within the window, which leads to a linear time complexity.

Space Complexity: O(1)

The space complexity is constant, as the solution uses a fixed number of variables to track the current window’s characteristics and the minimum swaps needed.

def minSwaps(self, data: List[int]) -> int:
    n = len(data)
    k = data.count(1)
    if k == 0:
        return 0
    left = right = 0
    zeros = 0
    mini = n

    is_zero = lambda i: int(data[i] == 0)

    while right < n:
        # Expansion
        while right < n and right - left < k:
            zeros += is_zero(right)
            right += 1
        # Logic
        mini = min(mini, zeros)
        # Shrinking
        zeros -= is_zero(left)
        left += 1
    return mini

2134. Minimum Swaps to Group All 1’s Together II (Medium)¶

Solution

This problem extends 1151. Minimum Swaps to Group All 1’s Together (Medium) to a circular array setting, requiring the identification of the minimum number of swaps needed to group all 1’s in the circular array nums together. The solution leverages a sliding window approach, similar to the non-circular version, but with a crucial adjustment to accommodate the circular nature of the array.

To handle the circularity, the sliding window is allowed to wrap around the end of the array back to the beginning, effectively doubling the array length for the window traversal. This ensures all cyclic permutations are considered when calculating the minimum number of swaps.

Initial Check:

If there are no 1’s in nums, no swaps are needed, and the function returns 0.

Expansion:

Progress through the doubled array, incrementing the count of zeros within the window until it includes k elements, where k is the total count of 1’s in nums.

Logic:

Determine the minimum number of zeros within any window of size k across the circular array, translating to the minimum swaps required.

Shrinking:

Before advancing the window, decrement the zeros count if the leftmost element is a zero, using modular arithmetic to correctly handle the circular wrapping.

The function returns mini, the minimum number of swaps required to group all 1’s together in the circular array.

Analysis

Time Complexity: O(N)

Despite the circular array requiring consideration of wrapping windows, the effective traversal length is capped at twice the array length, maintaining linear time complexity.

Space Complexity: O(1)

Constant space is utilized, with a fixed number of variables tracking the window’s status and the running minimum swaps needed.

def minSwaps(self, nums: List[int]) -> int:
    n = len(nums)
    k = nums.count(1)
    if k == 0:
        return 0
    left = right = 0
    zeros = 0
    mini = n

    is_zero = lambda i: int(nums[i] == 0)

    while right < 2 * n:
        # Expansion
        while right < 2 * n and right - left < k:
            zeros += is_zero(right % n)
            right += 1
        # Logic
        mini = min(mini, zeros)
        # Shrinking
        zeros -= is_zero(left % n)
        left += 1
    return mini

Heap¶

while expand

239. Sliding Window Maximum (Hard)¶

Also

K Sized Subarray Maximum (Medium)

Solution

The approach utilizes a max heap to track the maximum value within each sliding window of the array. The heap stores tuples of (negative value, index) to mimic a max heap behavior because Python’s heapq implements a min heap by default.

Expansion:

Iterate through the array using a right pointer, adding each element to the heap as a tuple of its negative value and its index.
This ensures we can both keep track of the values’ ordering and efficiently retrieve the maximum value.

Logic:

Once the window size reaches k, check the top of the heap to determine the current window’s maximum value.

Shrinking:

Increment the left pointer to slide the window forward.
Pop elements from the heap if their indices are less than the updated left pointer, ensuring the heap’s top element always falls within the current window’s bounds.

Analysis

Time Complexity: O(N log N)

Each insertion and deletion operation on the heap takes O(log N), and we perform these operations for each element.

Space Complexity: O(N)

The heap may contain up to N elements, one for each element in the array.

def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
    n = len(nums)
    left = right = 0
    heap = []  # Max heap: elements stored as (-value, index)
    ans = []

    while right < n:
        # Expansion: Add new elements to the heap
        while right < n and right - left < k:
            heapq.heappush(heap, (-nums[right], right))
            right += 1

        # Logic: Append the current maximum to ans
        ans.append(-heap[0][0])

        # Shrinking: Ensure the top of the heap is within the current window
        left += 1
        while heap and heap[0][1] < left:
            heapq.heappop(heap)

    return ans

Sorting¶

while expand

1984. Minimum Difference Between Highest and Lowest of K Scores (Easy)¶

Solution

The aim is to find the minimum difference between the highest and lowest scores within any subset of k scores from the given array nums. This problem can be efficiently solved using a sliding window approach on the sorted array.

By sorting nums first, the problem simplifies to finding the smallest window of size k where the difference between the first and last elements (the lowest and highest scores within the window) is minimized.

The solution iterates through the sorted nums, maintaining a window of size k. For each window, it calculates the difference between the highest and lowest scores and updates mini to keep track of the minimum difference found.

Expansion:

Move through the sorted nums with a right pointer, expanding the window until it encompasses k elements.

Logic:

After reaching a window of size k, calculate the difference between the last and first elements in the window. Update mini if this difference is smaller than any previously recorded.

Shrinking:

Increment the left pointer to slide the window forward by one position, preparing to evaluate the next window of k elements.

The function returns mini, the smallest difference between the highest and lowest scores in any subset of k scores from nums.

Analysis

Time Complexity: O(N log N)

Sorting the array nums takes O(N log N) time. The subsequent sliding window operation to find the minimum difference runs in O(N), leading to an overall time complexity dominated by the sorting step.

Space Complexity: O(1)

The solution requires constant extra space, aside from the sorted version of the input array nums.

def minimumDifference(self, nums: List[int], k: int) -> int:
    nums.sort()
    n = len(nums)
    left = right = 0
    mini = float("inf")
    while right < n:
        # Expansion
        while right < n and right - left < k:
            right += 1
        # Logic
        mini = min(mini, nums[right - 1] - nums[left])
        # Shrinking
        left += 1
    return mini

Bit Manipulation¶

while expand

3023. Find Pattern in Infinite Stream I (Medium)¶

Solution

This problem involves identifying the starting index of a given binary pattern within an infinite stream of bits. The solution leverages bitwise operations to maintain and compare the current sequence of bits in the stream against the target pattern, using a sliding window concept to dynamically adjust the sequence being considered.

A key aspect of the solution is the conversion of the binary pattern into an integer (target) for efficient comparison. The algorithm iterates through the stream, constructing an integer representation of the current sequence of bits (current) of the same length as the pattern. This allows for direct comparison between the current sequence and the target pattern.

Expansion:

Incrementally add bits to the current sequence by shifting it left and appending the next bit from the stream until the sequence matches the length of the target pattern.

Logic:

Once the current sequence reaches the length of the pattern, check if it matches the target. If a match is found, return the starting index of the sequence in the stream.

Shrinking:

To move the window forward and consider the next sequence, remove the leftmost (most significant) bit from current. This is achieved by first ensuring the leftmost bit is set (using | mask) and then removing it with an XOR operation (^ mask).

The function findPattern iterates through the stream, continuously updating the current sequence and comparing it to the target pattern until a match is found or the stream ends.

Analysis

Time Complexity: O(N)

Where N represents the number of bits read from the stream until the pattern is found. The complexity is linear relative to the distance in the stream at which the pattern occurs, as each bit is processed once.

Space Complexity: O(1)

Constant space is used, as the solution employs a fixed number of variables (left, right, target, current, and mask) to manage the window and perform the comparison, independent of the stream’s length or pattern size.

def findPattern(self, stream: Optional["InfiniteStream"], pattern: List[int]) -> int:
    k = len(pattern)
    left = right = 0
    target = current = 0

    for i in pattern:
        target = target << 1 | i

    while True:
        # Expansion
        while right - left < k:
            current = current << 1 | stream.next()
            right += 1
        # Logic
        if current == target:
            return left
        # Shrinking: Trim the left most (most significant) bit
        mask = 1 << (k - 1)
        current = (current | mask) ^ mask
        left += 1

3037. Find Pattern in Infinite Stream II (Hard)¶

Solution

Literally same as 3023. Find Pattern in Infinite Stream I (Medium), but with slightly different constraint:

1 <= pattern.length <= 10000 instead of 1 <= pattern.length <= 100

Analysis

Time Complexity: O(N)

Space Complexity: O(1)

def findPattern(self, stream: Optional["InfiniteStream"], pattern: List[int]) -> int:
    k = len(pattern)
    left = right = 0
    target = current = 0

    for i in pattern:
        target = target << 1 | i

    while True:
        # Expansion
        while right - left < k:
            current = current << 1 | stream.next()
            right += 1
        # Logic
        if current == target:
            return left
        # Shrinking: Trim the left most (most significant) bit
        mask = 1 << (k - 1)
        current = (current | mask) ^ mask
        left += 1

Miscellaneous¶

while expand

30. Substring with Concatenation of All Words (Hard)¶

Solution

This problem seeks substrings in s that are exactly the concatenation of all words in the array words, with each word appearing exactly once. The solution employs a sliding window approach, iterating through s with multiple starting points to accommodate different alignments of concatenated words.

Each window aims to capture a substring of length equal to the total length of all words combined (k). A needed counter tracks the frequency of words required to form a valid concatenation.

Expansion:

The window expands by examining segments of s of length equal to a single word (word_len), decrementing the count of the encountered word in needed. If a word’s count drops to zero, it is removed from needed, indicating it has been fully matched.

Logic:

If needed becomes empty, it signifies all words have been matched in the current window, and the starting index is added to ans.

Shrinking:

The window shrinks from the left by incrementing the count of the leftmost word and moving the left boundary forward by one word’s length. This prepares for the next potential match.

The function iterates through s with starting points varying from 0 up to word_len - 1 to ensure all possible concatenations are considered.

Code Commentary

The sliding_window function is called for each possible starting point within the length of a single word to account for different alignments. The function uses a needed counter to track the frequency of words that need to be found within the current window. As the window expands, words are checked against needed, and if a complete set of words matches, the starting index of that window is recorded. The window then shrinks to move forward and search for new matches.

Analysis

Time Complexity: O(L * (M + N))

The algorithm iterates up to L times for each potential starting point within a word’s length, where L is the length of each word. For each starting point, it scans through the string s (N) and performs operations for matching words which, cumulatively over all iterations, are proportional to the total length of all words combined (M). Therefore, the overall time complexity reflects the product of the number of starting points and the operations performed per start point.

Space Complexity: O(M + N)

The space complexity is determined by the storage required for the needed counter and the ans list. The needed counter’s size is proportional to the number of unique words in words (M), and the ans list could theoretically hold a starting index for every position in s (N), leading to a combined space requirement.

def findSubstring(self, s: str, words: List[str]) -> List[int]:
    def sliding_window(start_from):
        left = right = start_from
        needed = collections.Counter(words)

        while right < n:
            # Expansion: Expand the window to the right to include new words
            while right < n and right - left < k:
                word = s[right : right + word_len]
                needed[word] -= 1
                if needed[word] == 0:
                    needed.pop(word)
                right += word_len  # Move the right pointer to the next word

            # Logic: Check if the current window forms a valid concatenation
            if needed == {}:
                ans.append(left)  # If needed is empty, all words are matched

            # Shrinking: Shrink the window from the left to search for new matches
            word = s[left : left + word_len]  # Word exiting the window
            needed[word] += 1
            if needed[word] == 0:
                needed.pop(word)
            left += word_len  # Move the left pointer to the next word

    n = len(s)
    word_len = len(words[0])  # Length of each word in the words list
    k = len(words) * word_len  # Total length of the concatenated words
    ans = []

    # Initialize the sliding window from each possible starting point within a word length
    for i in range(word_len):
        sliding_window(i)

    return ans

Fixed Window¶

Naïve Sum/Average¶

Hashmap¶

Hashmap - Duplicate Elements¶

Generic Solution: Find Duplicates within Window Size k¶

Hashmap - Unique/Distinct Elements¶

Hashmap - Anagrams/Permutations¶

Count¶

Count - Math¶

Count - Swaps¶

Heap¶

Sorting¶

Bit Manipulation¶

Miscellaneous¶

Generic Solution: Find Duplicates within Window Size `k`¶